24 June, 2022

I build businesses, both as independent startups and as new initiatives within large global companies. This series of posts is based on an FX Options training course that I delivered whilst contributing to building FX businesses at a number of investment banks. If you are looking to build a business and require leadership then please contact me via the About section of this website.

FX Options Guide - Section 13 - Knockout Option Risk Management Considerations

Knockout Option Risk Management Considerations Introduction

In this section we continue our look at barrier options by looking at risk management considerations to start to build our intuition of knockout options. To get the most from this section you should first have covered the sections on knockout options and the knockout option pricing examples.

Knockout Options – Risk Management Considerations

The following relationship is always true:

So, assuming we are describing knockouts which have the same expiration, strike, barrier and are the same class of option (i.e. call/put), we can describe the knockout in the following way,

Describing a knockout as the difference between a standard and a knockin helps us to gain intuition.

Note that the same relationship applies to reverse knockout options and reverse knockin options that we will see in later sections.

Sensitivity To Location Of Barrier

For a knockin option to make money, spot must move in the direction of out-of-the-money, trigger the barrier, then spot must turn around to finish in-the-money. The further spot must travel to trigger the barrier, the less likely the barrier will be triggered, and therefore the lower the value of the knockin option. If the price of the knockin option is going lower then the price of the knockout option is going higher. In other words, the probability of hitting the barrier, and then finishing in-the-money is the key. The higher the probability of hitting the barrier, the higher the value of the knockin, and the lower the value of the knockout.

Consider the following: 6 month, EUR call / USD put, strike 1.1400, spot 1.1406.

Compare this standard option to the equivalent knockout, varying the barrier between 1.1300 and 1.0400.

Sensitivity To Location Of Barrier And Time To Expiration

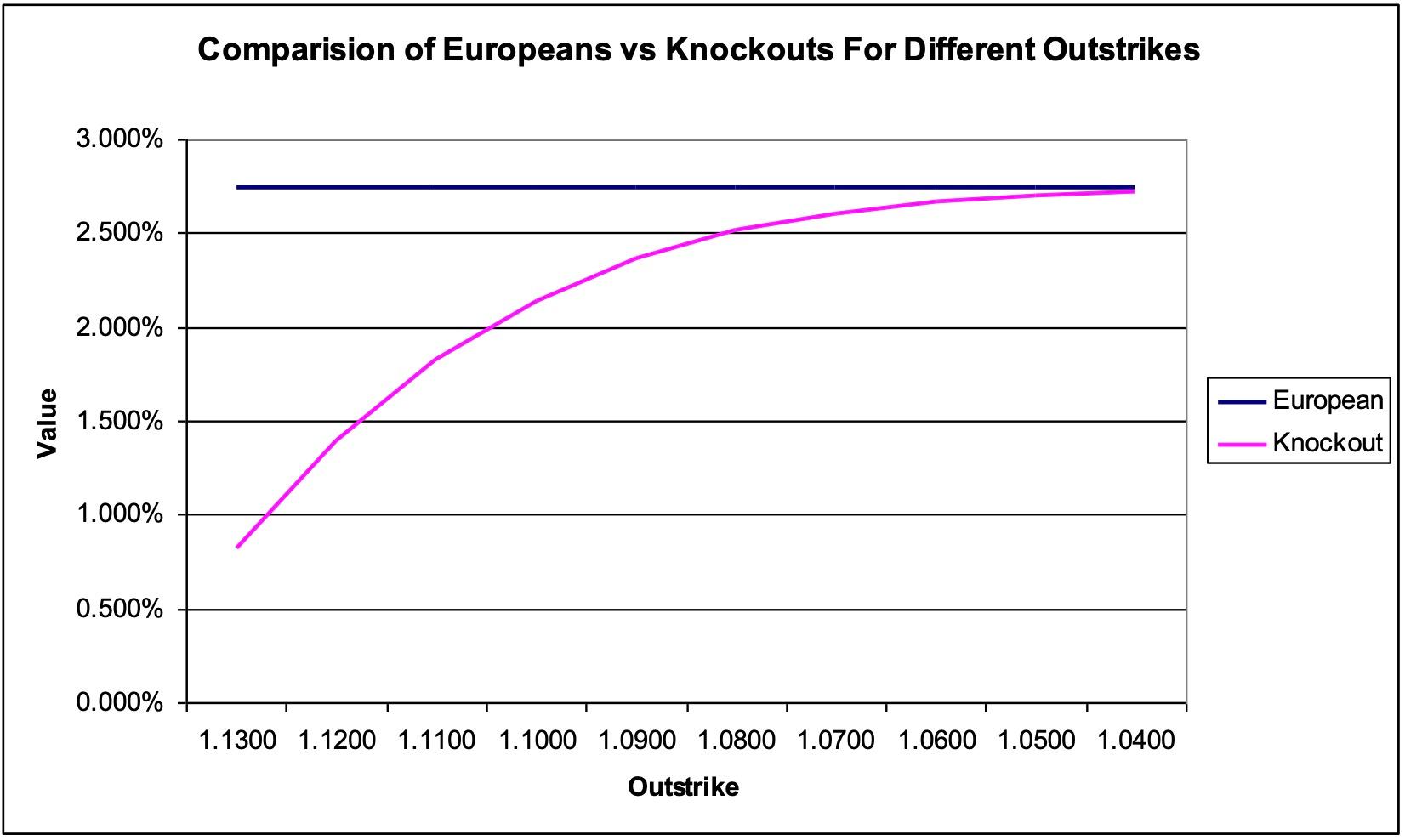
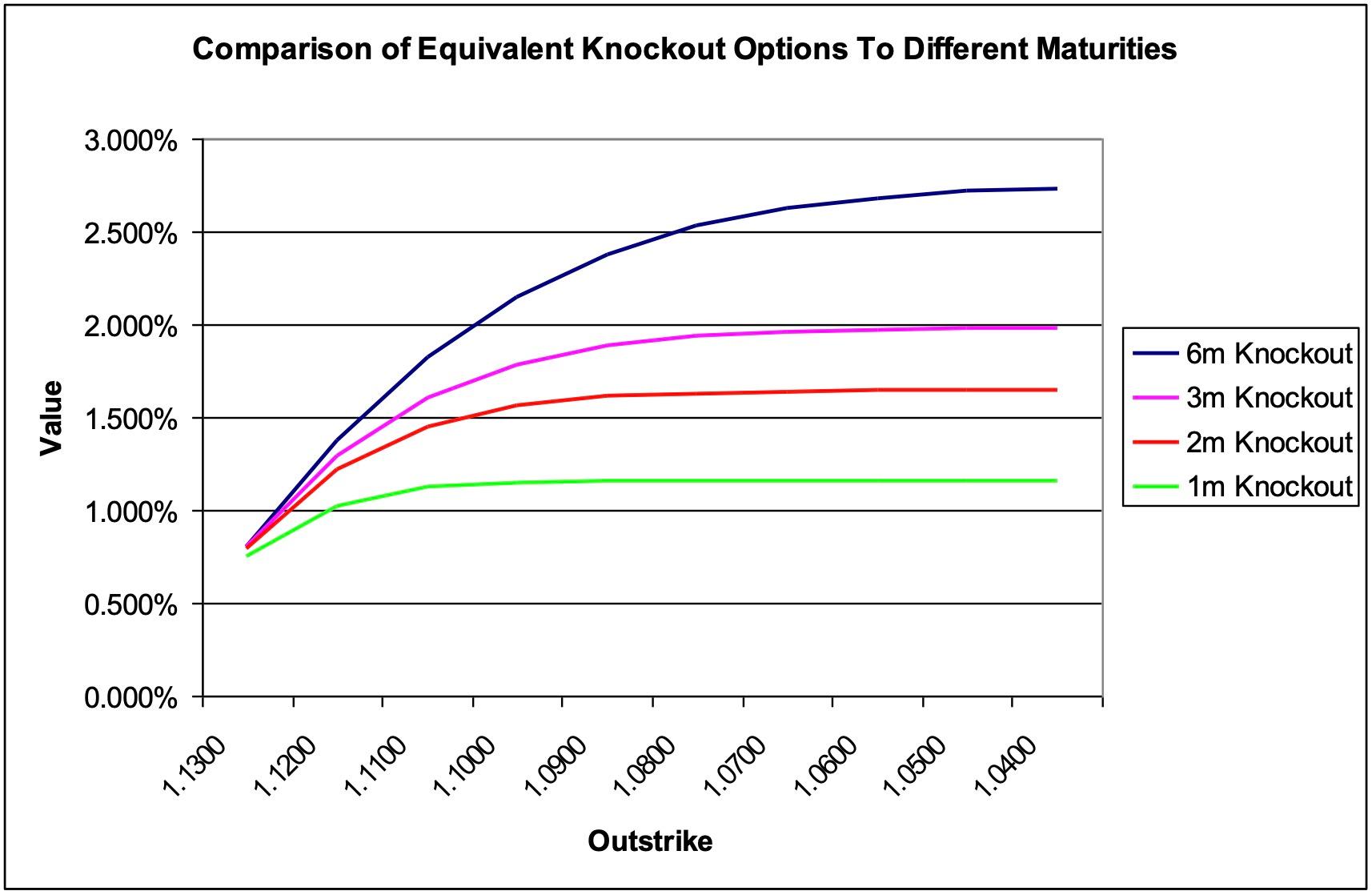
Now consider the same example, but for different maturities. As the time to expiration increases, the value of a standard option increases. Since the boundary condition for the knockout option is such that its value cannot be greater than the equivalent standard option, then as the barrier moves further away from initial spot the value of the knockout option will tend towards a higher boundary condition. As the barrier is set closer to initial spot, the value of the knockout option to any maturity will tend towards zero. Therefore, it can be seen that the rate at which the value of the knockout option changes relative to the distance between the barrier and initial spot is greater for longer dated options. This is described in the diagram below.

Sensitivity To Volatility

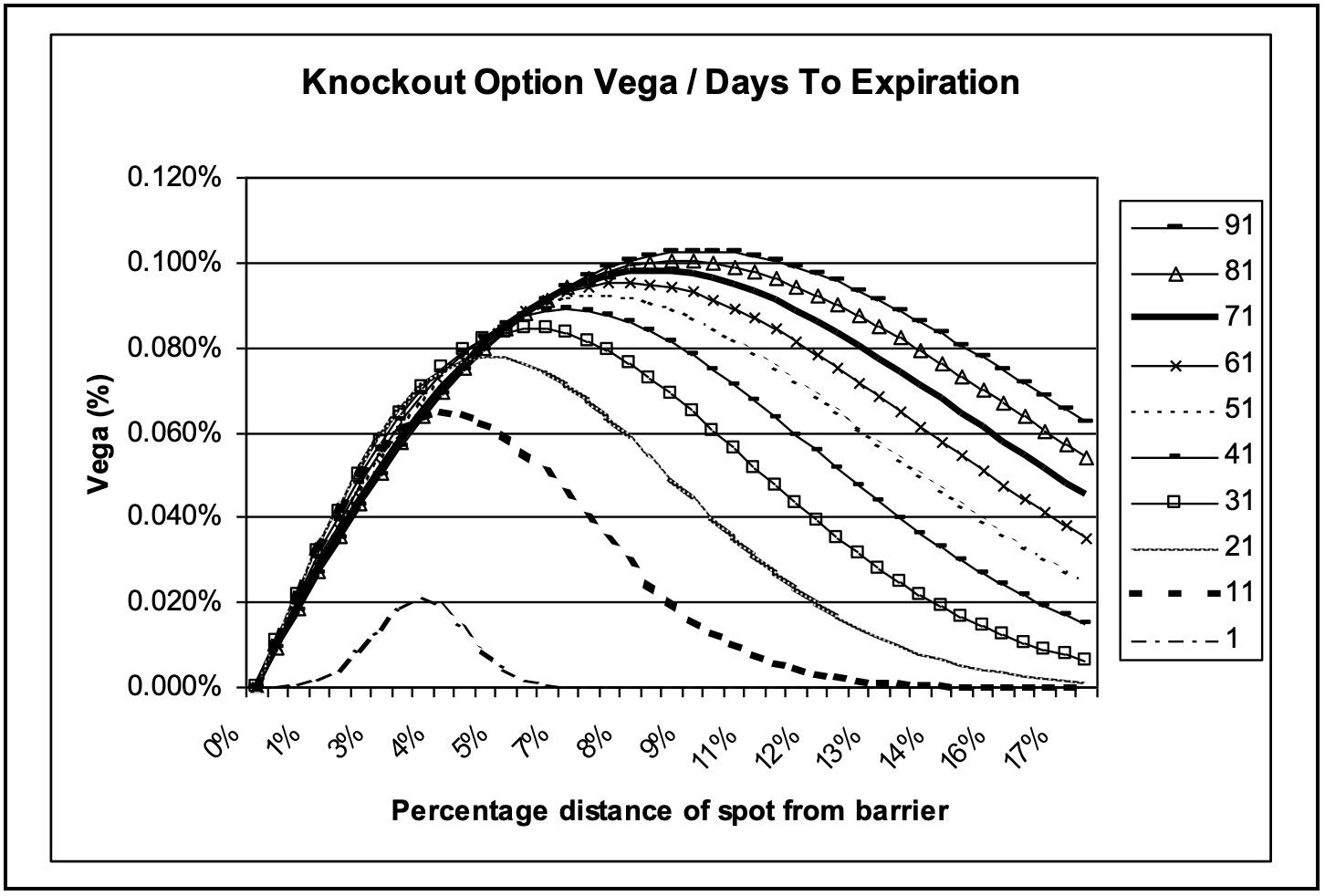
As volatility increases, the probability of triggering the instrike is increased, and therefore the value of the knockin increases. That is, the knockin option has positive vega. Given the expression above, that is, the value of the knockout can be considered to be the difference between the value of the standard, and the knockin, then we can see that the knockout option has less vega than the standard option. Indeed, it is possible, in exceptional circumstances, for the knockin vega to exceed that of the standard, therefore it is possible for the knockout vega to go negative.

Sensitivity To Spot

As spot gets closer to the barrier, the rate at which the knockout option loses value is much greater than the rate at which the equivalent standard option loses value. This means that the change in the value of the knockouts value for a given change in spot value is greater. That is, the delta of the knockout option is greater than the delta of the equivalent standard option. This is true in all cases except where spot is so far away from the barrier that the knockout behaves identically to the standard option.

Knockout Versus Risk Reversal

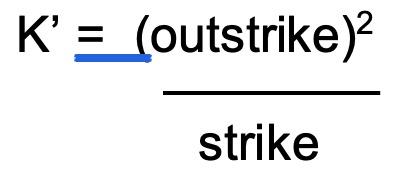
To gain further intuition about the knockout option it is instructive to compare the knockout to a risk reversal. The way in which the barrier is monitored for a knockout is by observing spot on a twenty-four hour basis. If spot trades at or beyond the barrier level then the knockout is terminated. If we were to observe the outright forward rate instead of the spot rate then we could hedge the knockout using a risk reversal. This assumes we would be able to close out the risk reversal at no cost at the time the barrier is triggered. One leg of the risk reversal would be the equivalent standard option of the knockout. The other leg of the risk reversal would have the strike price, known as the ghost strike, k’, as follows:

First consider the profile of a short standard option position:

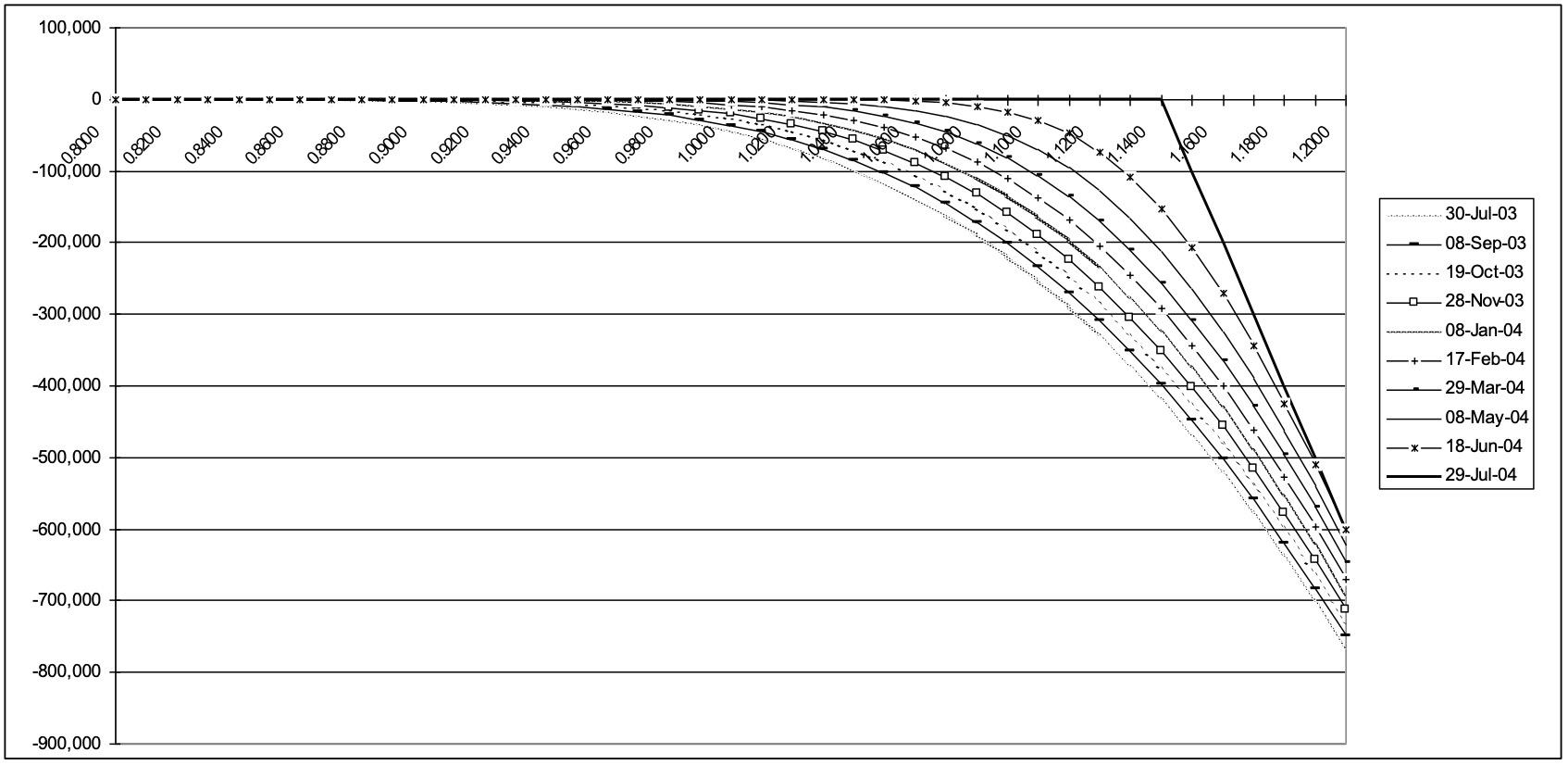
Now consider the profile of a short knockout option position:

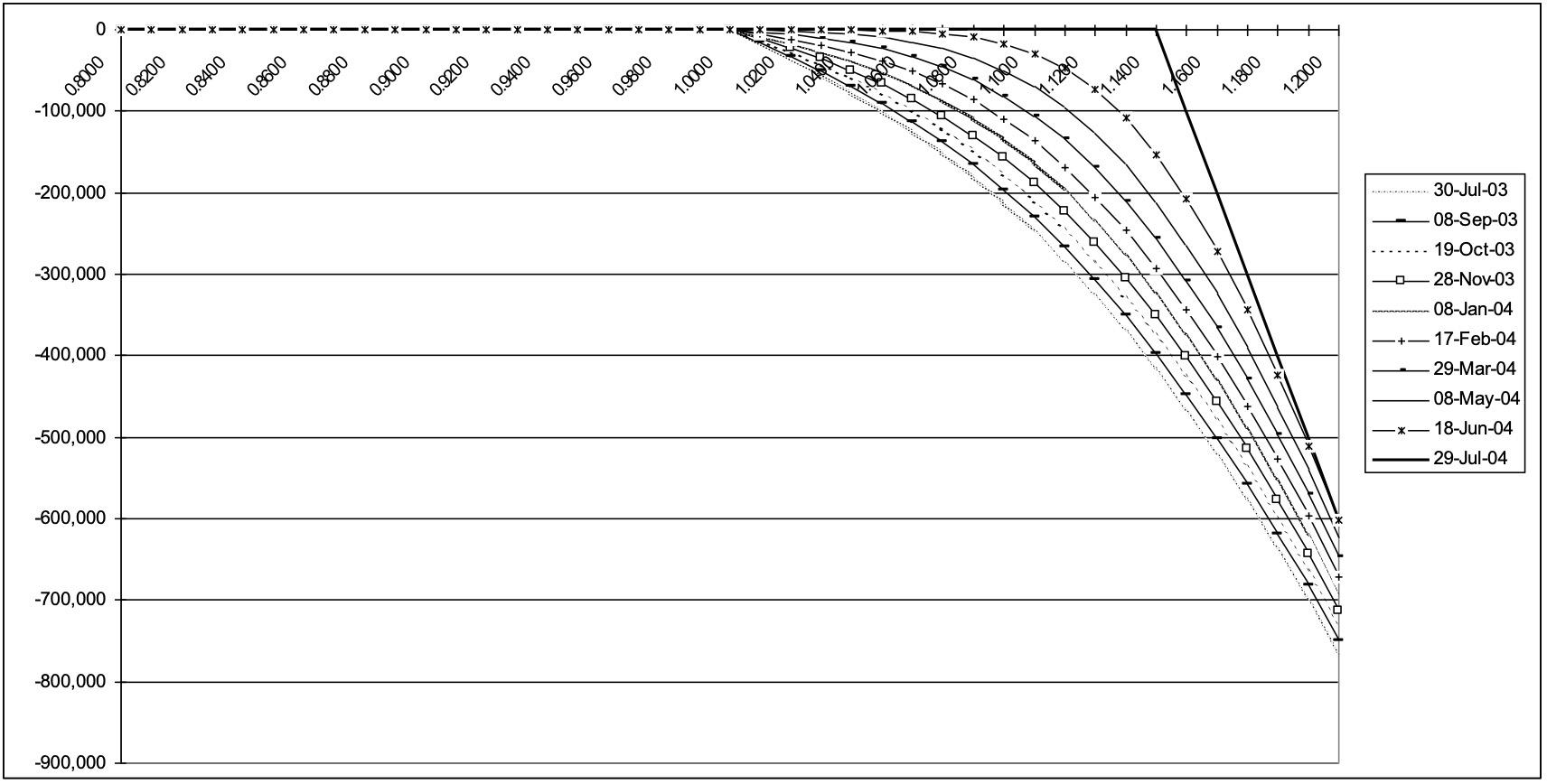
Finally, consider the profile of the risk reversal:

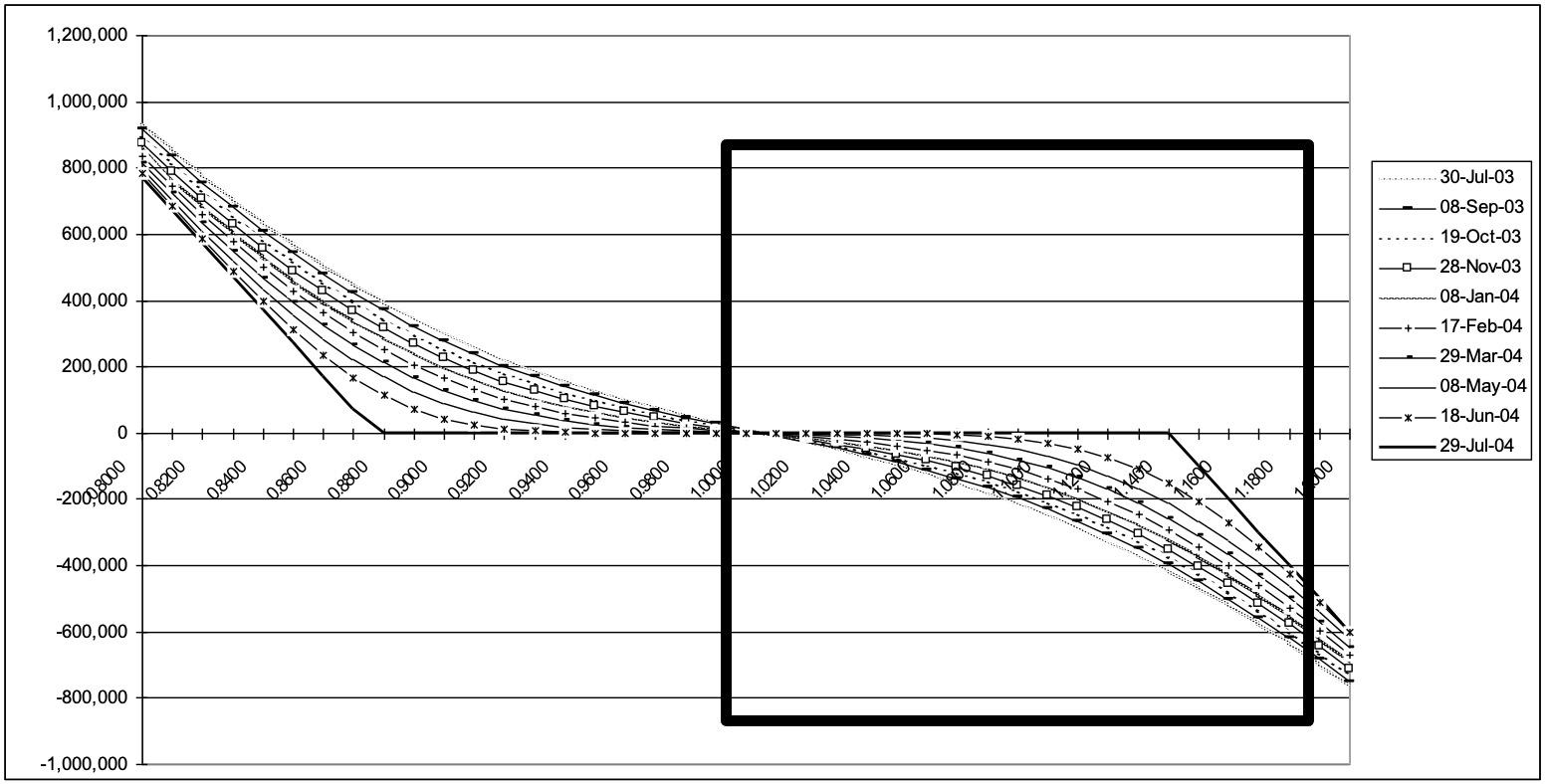
Note that for the risk reversal short leg, prior to the point where the value crosses the x-axis (as highlighted by the box) looks very similar to the profile of the knockout option.

Given the similarity between the risk reversal and the knockout option it is clear that the knockout option price must be sensitive to the skew in volatility between puts and calls. Indeed, it is unclear as to which volatility should be used to calculate the price of the knockout, as standard valuation models only allow a single volatility input. Clearly, the standard model is inadequate for accurate valuation of knockout options.

Knockout Options And The Term Structure Of Interest Rates And Volatility

The knockout option is path dependent, i.e. unlike a standard option which is sensitive only to where spot is trading at expiration, the knockout option is sensitive to the path that spot takes from inception of the trade, until expiration. This is because the barrier can be triggered at any time the spot market is open. The standard valuation model for pricing knockout options accepts only a single volatility, which corresponds to some volatility to the maturity of the option. If a knockout option has a maturity of one year, and the one year volatility is, say, 10%, but the one month volatility is 15%, then it is clear that the standard valuation model using the 10% volatility would under-estimate the probability of being knocked out during the first month. If the probability of being knocked out is under-estimated then the value of the knockout will be too high. Similar arguments apply to the forward curve implied by the term structure of interest rates, and the effect it may have in increasing or decreasing the probability of being knocked out. Once again, this highlights the deficiencies of the standard valuation model for knockout options.

Next Section - Knockin Option

In the next section we continue our introduction to barrier options by looking at the knockin option.

---