4 March, 2022

FX Options Guide - Section 5 - Options Valuation

Options Valuation Introduction

In this section we start to cover both the intuition and the detail of the how to calculate the price of an fx option. This will be of particular importance in later sections when we cover how a salesperson at at investment bank might go about executing an fx option on behalf of a client. To get the most from this section you should first have covered the foundational knowledge including the terminology of FX options and looked at some common option strategies. You should also have covered how options are funded and how these funding techniques are used when combining options.

Options Valuation & The Option Pricing Formula

An option is worth the expected value of its future payoff (future parity – “parity” is the name given to the intrinsic value in the option, i.e. for a call option the difference between spot and strike). The option pricing model answers the question: What is the most probable parity value of the option at expiration? That amount, discounted to the present, is the premium of the option.

If an event has more than one possible outcome, the expected value of the events is the sum of the individual expected values. For example, if a given instrument has a 40% chance of returning $100, and a 60% chance of returning $175, its expected value is:

0.40 x (100) + 0.60 x (175) = $145, and $145 should be its price in the market.

Extrinsic Value

Extrinsic value can be thought of as the numerical value of the uncertainty that the option might be exercised. That uncertainty is a function of:

1. How far must the market go before it crosses the strike price (how deep in-or out-of-the-market is it)
2. How much time remains for that movement to occur
3. How volatile is the market expected to be during that period

If probabilities determine the values of options, what determines the probabilities?

• Expected volatility in the cash market
• Time remaining in the option

There are two keys to option pricing:

1. The size of the distribution curve (which is determined by expected volatility and time to expiration)
2. The relationship between the centre of the distribution (i.e., the forward outright price) and the option strike price

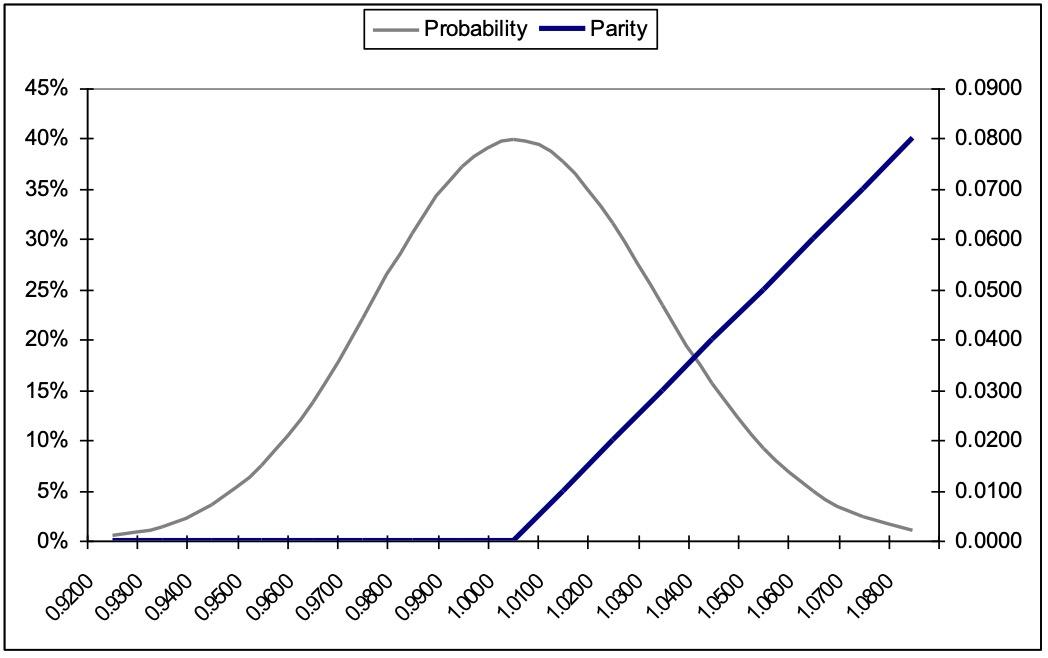
Consider an At-The-Money-Forward call option in terms of parity and probability:

Now consider an Out-of-The-Money call option in terms of parity and probability:

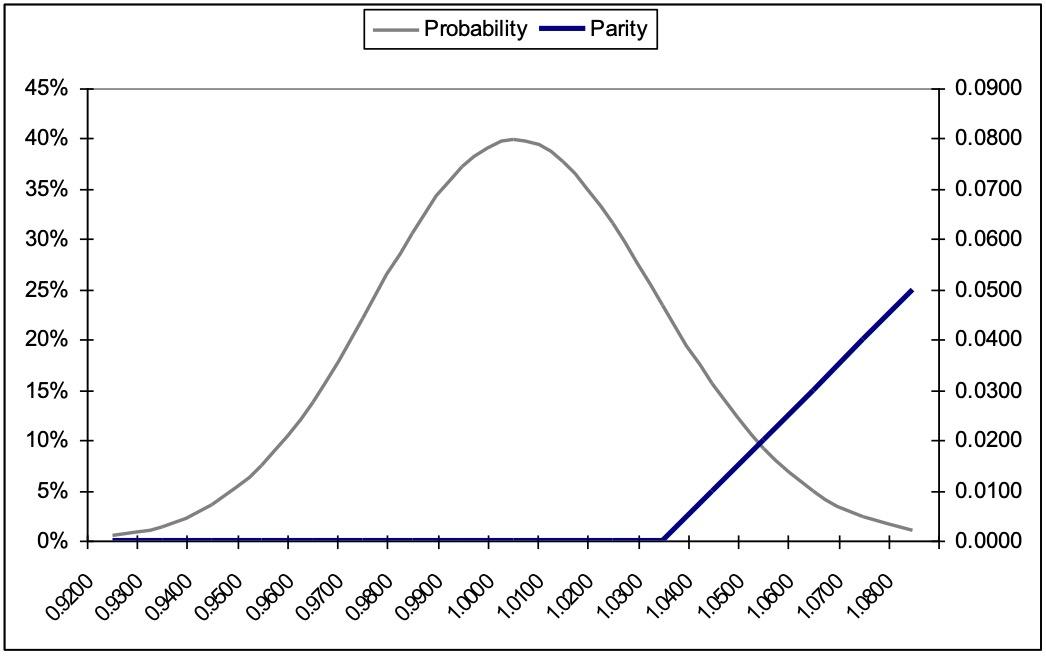
The values of the two options are represented by the area under the probability curve multiplied by the parity value of the options. The difference between the two options is the strike price. That determines what probability levels the various parity amounts are multiplied by. As can be seen, for the ATM options parity is multiplied by much higher probabilities. Therefore the theoretical value of the option is higher. The OTM option has the same upside potential, but the probability of reaching these levels is negligible and that is reflected in a lower theoretical value.

Theoretical Option Valuation Models

If you quote the premium in terms of volatility, then you must be agreeing about the model underlying the valuation and every other input to the model. There is a one-to-one correspondence between volatility and option premium.

What do you need to value an option? Contract specifications:

• Call or Put
• European or American
• Strike Price (K)
• Time or Expiration Date (t)
• Face Amount
• Where is the underlying trading [Spot (S)]
• Interest Rates [where is Spot headed (r1, r2)] or the Forward (F)
• What is the exchange rate’s Volatility (σ)

Option Risk Measures

Delta (Δ): The change in the option value given a change in price or rate of the underlying (the hedge ratio)

Gamma (Γ): The change in the delta given a change in the underlying price or rate (curvature)

Vega (V): The change in the option value given a change in the volatility of the underlying

Theta (θ): The change in the option value as time passes (time decay)

Rho (ρ): The change in the option value given a change in interest rates

Next Section - Option Risk Characteristics

In the next section we continue our introduction to FX options by looking at option risk characteristics.

---