Take Your Learning to the Next Level! See More Content Like This On The New Version Of Perxeive.
Get Early Access And Exclusive Updates: Join the Waitlist Now!
1 April, 2022
FX Options Guide - Section 7 - Gamma
Your Goals In This Section
The intention of this section is to give you a the knowledge of gamma that will enable you understand what it is and why it is important to fx options traders.
Your goals by the end of this section are to be able to:
- Describe what gamma is
- Explain how traders use gamma to generate profits
- Determine a traders view of short term market volatility through knowledge of whether the trader is long or short gamma
Choose Your Path To Achieving The Section Goals
Setting you up to acheive the goals of this section is our goal. Having some knowledge of the pricing of standard European options and their risk characteristics, if you are not yet familiar with them, would help you achieve the section goals.
- If you are already familiar with the pricing of standard European options and their risk characteristics, then continue reading
- If not, and you want to cover this first the you will find the links to the relevant sections here...
Gamma Introduction
Gamma is a key derivative of an option that represents the change in the delta of an option with respect to a change in spot. It is also sometimes referred to as the convexity of the option with respect to spot.
Gamma tells an options trader by how much the delta of an option, or a portfolio of options, will change for a given move in spot. Since option traders delta hedge their portfolios, gamma tells them the amount of the spot trade they will need to execute in the market for a given move in spot in order that their option or portfolio of options remains delta hedged.
The gamma of an option increases as the time to expiration decreases. That is, gamma is greatest:
- The closer the option is to expiration
- The closer spot trades to the strike price of the option
The FENICS chart below shows the gamma of options around the strike price for different maturities over a range of spot values:
Gamma And The Dynamic Delta Hedging Of Options
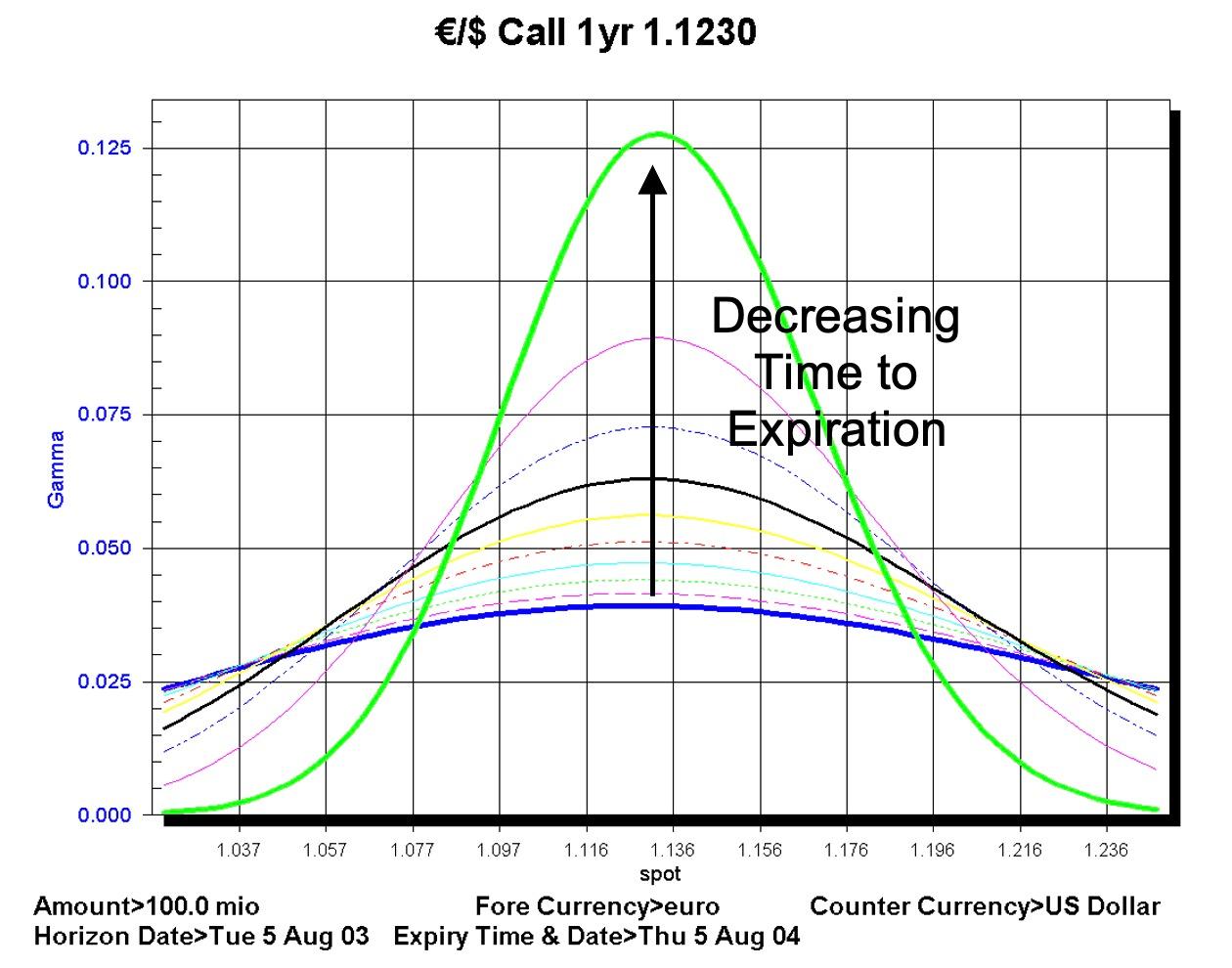
Options traders are trading the volatility of the option not the underlying spot and so keep their portfolios delta hedged. As spot changes gamma tells the trader how much spot needs to be bought or sold in order to hedge the portfolio. It is instructive to take a simple, single option example to demonstrate the dynamic delta hedging of options.
The FENICS pricing page below shows a one week EUR call / USD put option on a face amount of EUR 100m. The option is an ATM option:
Note that the delta amount is EUR 49.04m if we buy the option. If we buy this EUR call option we would be long EUR through the option. To delta hedge this option we would need to sell EUR’s. In this case we would sell EUR 49m at 1.1350 USD per 1 EUR.
As spot moves to 1.1400 the delta changes to EUR 62.42m. We are now long EUR 62.42m through the option and short EUR 49m on the hedge. To flatten our delta we need to sell EUR 13.5m at 1.1400.
If spot now moves to 1.1450 the delta changes again. The delta of the option has changed to EUR 74.16m. So, we are now long EUR 74.16m through the option and against that we are short EUR62.5m on the hedge. To return to delta nuetral we need to sell EUR 12m at 1.1450.
Spot now moves higher again to 1.1500:
The delta of the option has reached EUR 83.3m. We are long EUR 83.3m through the option and short EUR 74.5m on the hedge. So we need to sell a further EUR 9m at 1.1500.
So as spot moves higher the option moves more in the money, the delta of the option has increased and in order to stay delta hedged we have sold more EUR’s spot.
Now consider what happens as spot starts to weaken. If spot were to fall from 1.1500 back down to 1.1450 the delta of the option would return back down to EUR 74.16m. So we would be long EUR 74.16m through the option but short EUR 83.5m on the hedge. So, in order to rebalance our portfolio we would need to buy EUR 9m at 1.1450.
Spot continues to fall back down to 1.1400. The delta of the option returns to EUR 62.42m. So we are long EUR 62.42m through the option but short EUR 74.5m on the hedge. To return to a flat delta position we need to buy EUR 12m at 1.1400.
Lets look at those last two spot transactions. The EUR 9m that we bought at 1.1450 we had previously sold at 1.1500. The EUR 12m we bought at 1.1400 we had previously sold at 1.1450. So as spot moves up and down and we re-hedge our delta position we are making money! If spot continues to move up and down before the option expires then we continue to make money.
This is because we are long the option. If we were short the option we would be doing exactly the opposite trades. Therefore if we were short the option we would lose money as we re-hedged our delta position as spot moves up or down.
So why wouldn’t we always stay long options? What is the catch? Well, there is one cashflow that we have ignored so far in this analysis and that is the initial premium. In the case of a long option we have paid out a premium. If we had sold the option we would have received the premium. So the ultimate P/L on the trade is the difference between the premium and the proceeds of the dynamic delta hedging.
The theoretical value derived from the Black-Scholes pricing formula represents the expected value of maintaining a constantly hedged portfolio. Therefore for an options trader if the implied volatility used to price an option at inception is, say, 10% and the realised volatility over the period of the option turned out to be exactly 10% then ignoring transaction costs the premium and the proceeds of the dynamic delta hedging would exactly off-set each other.
The Black-Scholes model has a number of assumptions including the assumption that there are no transaction costs. What does this mean for options? Clearly transactions costs cause additional costs to option traders. The bid/offer spread of the two way volatility price will reflect the transaction costs from trading gamma. That is, the wider the spot (and forward) prices in the underlying, the wider the volatility quote needs to be.
Long Gamma / Short Gamma
When option traders say they are long gamma they are telling you something. As we noted above, short dated options have the most gamma. Also, we noted above that options close to the strike price have the greatest gamma. We have seen that being long an option and therefore long gamma results in gains when dynamically delta hedging. So a trader who is long gamma is long short dated options, with strikes close to current spot. Clearly the trader is expressing the view that they expect spot to move around by more than implied by the volatility at which they bought the gamma options.
The converse is true of traders who are short gamma. Clearly a trader who is short gamma expects stability in the underlying market.
Congratulations on Levelling Up On Gamma!
Congratulations on making it to the end of this section. Gamma represents a relatively complex financial derivative concept and having a solid foundational knowledge of gamma sets you on the path to a much deeper understanding of the FX options market.
You have earned yourself the choice of taking on the challenge of getting to the next level up or sitting back and enjoying the moment of your new achievement:
Gamma - Useful Background Knowledge
To better understand gamma it is helpful to have a good grounding in options valuation and option risk characteristics..